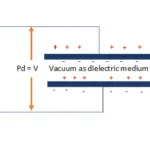
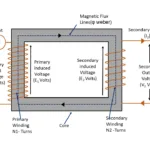
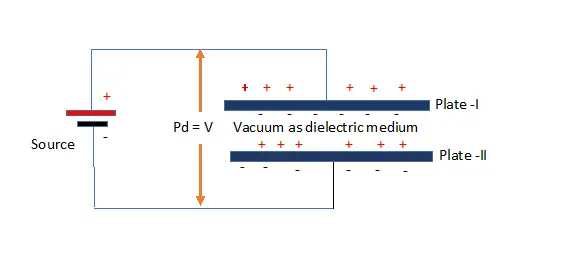
When potential difference applied between two conducting surface separated by an insulator (dielectric medium), electrical energy stored in both conducting surface. This property called as capacitance. The device fabricated such method to store electrical energy known as capacitor.
Capacitance always denoted by C.
Unit of capacitance known as farad (F).
Definition of farad
A capacitor is said have one farad capacitance, if it can able to store electric charge (Q) of one coulomb when potential difference applied by external source one volt (1V) between both conducting surface.
Factors depends on capacity of capacitor
All capacitors are does not store same electrical energy for same dimension of fabrication. It depends upon below listed parameter
- Geometrical dimension of capacitor like area, width of plates
- Type of conducting medium used for plates
- Physical property of conducting medium
- Dimension of di electric material inserted between plates
- Chemical properties of di electric material
- Atmospheric condition where capacitors are used
By consider above factors geometrical dimension like area of plates and distance between plates can be modified while fabrication. So capacitance of a capacitor can be simply said as

Where
ε0 = Relative permittivity in free space
εr = Relative permittivity in vacuum
A = Area of plate in square metre
D = Distance between plates in metre
Further we know that charge stored in both parallel conducting plates is always proportional to applied voltage between them capacitance of it (Capacitance depends on geometrical dimension of plates and chemical properties of dielectric material).
The charge store in a capacitor (Q) = CV coulomb
So capacitance of a capacitor (C) = Q/V farads
Different capacitor may store more or lesser amount of charge when same potential difference applied. So capacitance also charges accordingly
When potential applied between plates a small amount of current taken in place while store charge into it. It can be derived from current equation


Where q = cv equation substituted

This equation shows that voltage across capacitor plates cannot change instantaneously. It increases in derivative form while current flowing through it. It shows finite change in voltage (V) in time zero gives value of infinity for dv/dt. So practically capacitor current is impossible




Above equation shows that voltage appears across capacitor plates in depends on integral form of current flowing through it and its initial voltage condition. Further any infinite change in capacitor current, the integral term contribution to the capacitor voltage in time zero (V (0)) must be zero. Hence capacitor voltage also cannot change instantaneously. It is depending on integral form of current through it.
Power absorbed by a capacitor
When a capacitor connected into a circuit if definitely consume certain amount of power. The power consumed by capacitor can be derived as
Power absorbed = voltage across it x capacitor current
P=VI

Where

Energy consumed by a capacitor
If a capacitor continuously configured and in an operational in a circuit it definitely consumes certain amount of electrical energy
Energy absorbed = Power x time




But a capacitor never consume energy like resistor and transform into heat. It returns back to source whenever potential difference across terminal is collapsed or brought down to zero.
Simply says when we short a small capacitor terminal its energy released into short terminal. As same as when source voltage become less than voltage developed in capacitor, current flow takes in reverse direction and discharge it across source.