Short Circuit KVA in Power System

Power systems are affected by various types of faults such as open circuit faults, short circuit faults, and line-to-ground faults. Among these, short circuit faults have the most significant impact on the performance of power system networks. Therefore, it’s essential to consider them carefully, particularly through short circuit KVA in power system calculations

In a power system, all components are vulnerable to short circuit faults. When such a fault occurs, a large current flows through the affected components, potentially causing serious damage. To prevent this, it is crucial to accurately determine the current that would flow under short circuit conditions. Based on these values, appropriate components are selected during the system design process. The rating or capacity of each component depends on the expected level of short circuit current.

However, selecting components purely based on the maximum short circuit current can result in an overdesigned and bulky system. To avoid this, series impedance (Refer Current Limiting Reactors) elements are introduced into the network to limit the short circuit current. These impedances help control and reduce the current that flows through specific paths during fault conditions.

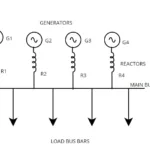
A Simple Network With Fault

For example, if a fault occurs at Point A in a network, the resulting current will naturally flow toward the path with the lowest impedance. Without any series impedance in the generator feeder line, a large surge of current may flow into the generators, potentially damaging them. However, by adding series impedance, this sudden surge is limited, protecting the generators by effectively isolating them from the faulty section.

Under normal conditions, impedances inherently limit short circuit currents to a significant extent. Components such as transformers, generators, and cables also function as effective reactive elements (reactors) in the system. Although these components possess some resistance, the reactance is much more dominant, especially during fault conditions.

In short circuit scenarios, reactance becomes 5 to 10 times greater than resistance, primarily due to the effects of harmonics and frequency disturbances. As a result, resistance is often considered negligible in short circuit current calculations, and the system is analysed primarily based on its reactive characteristics.

Reactance is typically expressed as a percentage, referred to as percentage reactance (%XL).

Definition of Percentage Reactance:

Percentage reactance is defined as the percentage of the total phase voltage that drops across the reactance of a component when full-load current flows through the circuit.

%X =(V_phI_ph)×100

   

in Transformers and Generators commonly derived as

[\ Percentage of Reactance (\%) = \frac{X_{actual} x I{FL}{V_{rated}} x 100\]

Reactance is typically represented as a percentage, denoted as %X

.Percentage of reactance %X = IX/V x100 [\ \%X = \frac{IX}{V}\]

Here,

I =  Full load current under short circuited condition

V = Phase voltage available in power system

X  =  Reactance connected in circuit Ohm/Phase

The percentage reactance can also be expressed in terms of kVA and kV, as derived from the above equation

By rewriting above percentage of reactance equation

   

Multiplying both numerator and denominator by Phase voltage V, we get

   

By diving voltage parameters in both numerator and denominator by 1000 , KVA can be obtained

   

   

   

This equation highlights that the percentage of reactance depends on the system’s KVA rating.

Now, let us assume that X represents the connected reactance in the circuit. Under short-circuit conditions, the short-circuit current can then be calculated as

   

By substitute the derivation of X in above, we get

   

In a power system, equipment typically comes with varying KVA ratings. As a result, determining the KVA for each individual component can be quite complex. To simplify calculations, the percentage reactance of all components is expressed using a common KVA rating, referred to as the Base KVA

The percentage of reactance at base KVA  =  KVA_Base/ KVA_Rated  X % Reactance at Rated KVA

The Percentage of reactance at KVA_base =

   

When a short circuit occurs, the voltage at the fault point drops to zero. It is standard practice to express the short-circuit current in terms of short-circuit KVA, calculated using the normal system voltage at the location of the fault

Short-circuit KVA is defined as the product of the normal system voltage and the short-circuit current at the point of fault

It is generally expressed in KVA

As we seen earlier in this article short circuit current Isc =  I (100/%X)

   

Power systems are typically three-phase systems. Therefore, to determine the short-circuit current in a three-phase system